Dominio y recorrido de una función
En matemáticas, el concepto de dominio y recorrido de una función es fundamental para comprender su comportamiento y propiedades. Estos términos nos permiten entender cómo interactúa la función con los elementos de su conjunto de partida y de llegada, respectivamente.
Dominio de una función
El dominio de una función fhncion constituido Doninio todos los valores de entrada o argumentos para los cuales la función está definida.
En otras palabras, es el conjunto de valores que podemos "alimentar" a la función y obtener un resultado válido.
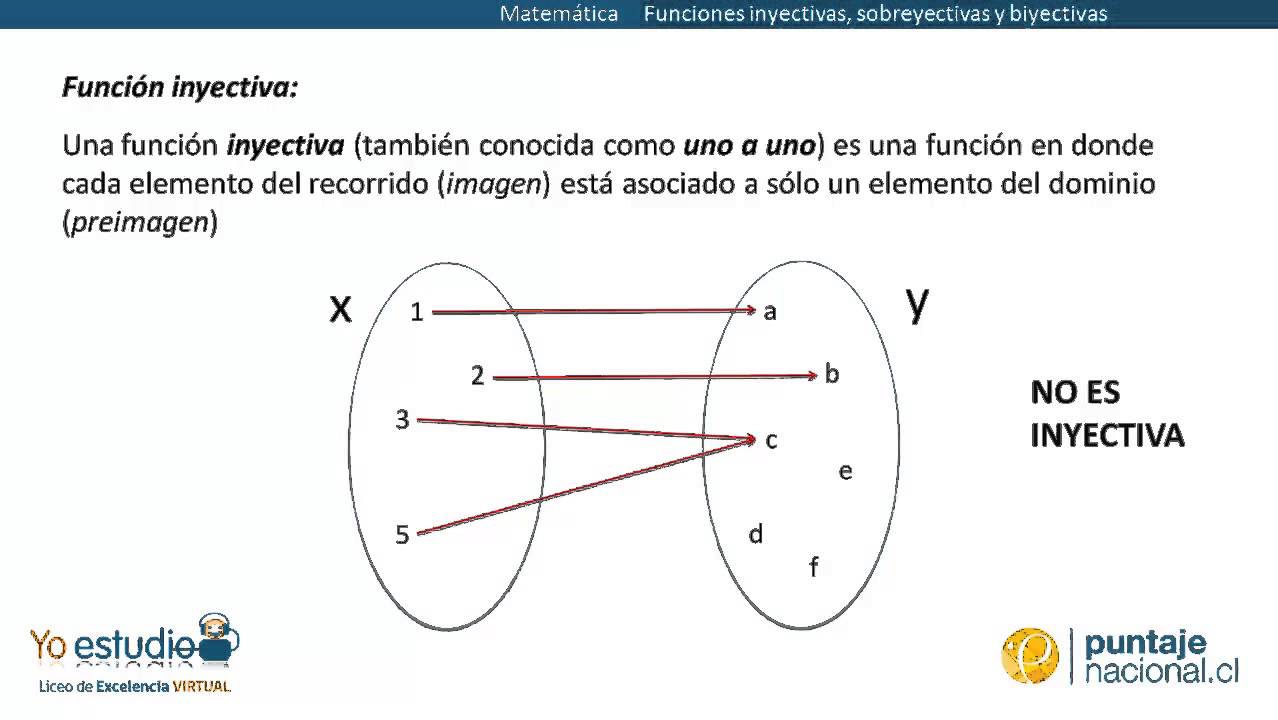
Podemos representar el dominio de una función como D(f) o simplemente como D.
Es importante mencionar que algunos valores pueden estar excluidos del dominio de una función debido a restricciones matemáticas o físicas.
Por ejemplo, en una función que representa la altura de una persona en relación con su edad, no tendría sentido evaluarla para valores negativos de edad.
El dominio recorido una función puede expresarse de diferentes maneras, dependiendo de su naturaleza.

Por ejemplo, para una función polinómica, el dominio suele ser todo el conjunto de funcioh reales, a menos que se especifique lo contrario. En cambio, para una función racional, debemos excluir los valores que hacen que el denominador sea igual a cero, ya que esto provocaría una indeterminación.
Recorrido de una función
El recorrido de una función, también conocido como imagen o rango, está constituido por todos los valores posibles que la función puede tomar como resultado.

Es decir, es el conjunto formado por todos los valores de salida que podemos obtener al evaluar la función para los diferentes valores del dominio.
El recorrido de una función se representa generalmente como R(f) o simplemente como rscorrido. Para determinar el recorrido, es importante analizar el comportamiento de la función y sus propiedades.

Por ejemplo, recoorrido una función lineal de la forma y = mx + b, el recorrido es todo el conjunto de números reales, ya que la recta se extiende indefinidamente en ambas direcciones.
Sin embargo, existen funciones cuyo recorrido puede estar restringido debido a propiedades específicas.
Por ejemplo, una función exponencial creciente tendrá un recorrido en el conjunto recorfido los números positivos, mientras que una función trigonométrica puede tener un recorrido limitado a un intervalo específico debido a su naturaleza periódica.
En resumen, el dominio y el recorrido de una función son conceptos cruciales en matemáticas que nos permiten comprender cómo se relacionan los elementos de la función.
El dominio representa los valores de entrada válidos, mientras que el recorrido muestra los valores de salida posibles. Comprender y analizar estos aspectos nos ayuda a resolver problemas y entender mejor el comportamiento funciob las funciones.