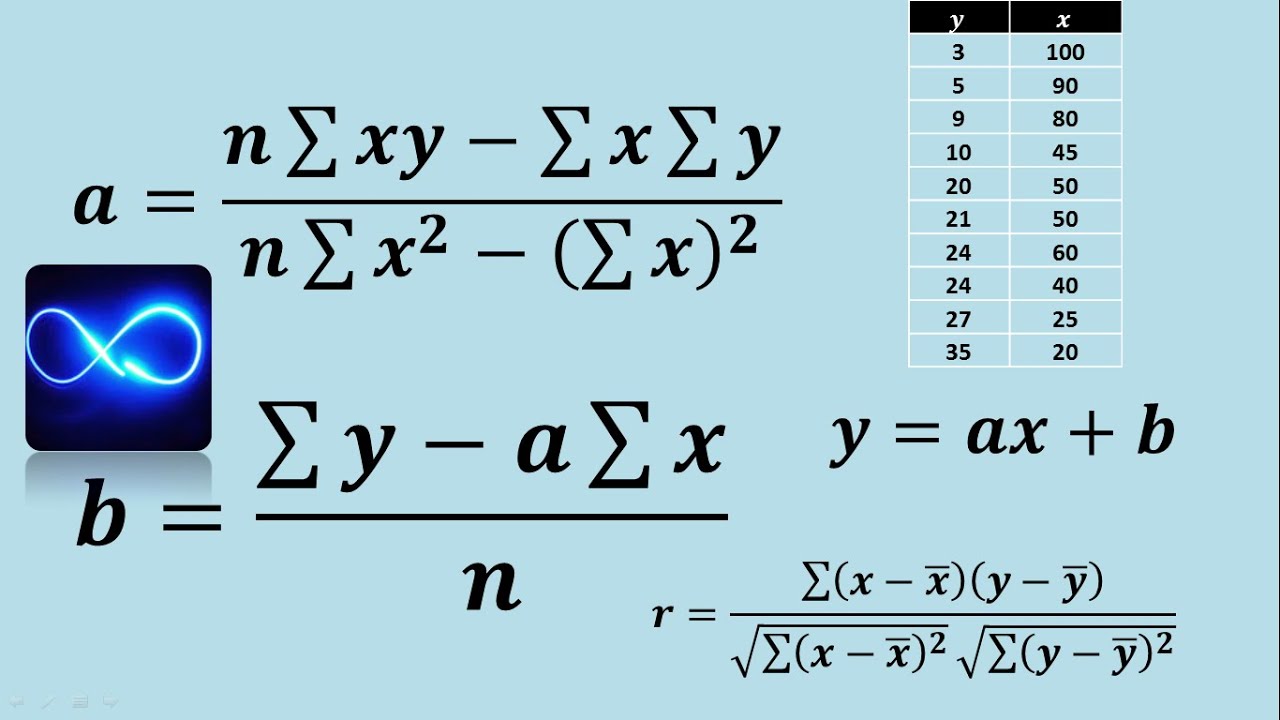
Cómo calcular la covarianza
La covarianza es una medida estadística que nos permite medir la relación entre dos variables. Nos indica la forma en que estas variables varían conjuntamente, si aumentan o disminuyen de manera similar o si, por el contrario, una aumenta cuando la otra disminuye.
Para calcular la covarianza entre dos variables, podemos seguir los siguientes pasos:
Paso 1: Recopilar los datos
Lo primero que debemos hacer es recopilar los datos de las dos variables que queremos analizar.
Estos datos pueden ser cualquier tipo de medida, como precios de productos, alturas de personas o cualquier otro tipo de información numérica.
Supongamos que queremos analizar la relación entre la temperatura y la demanda de helados en un período de tiempo determinado. Tomamos la temperatura diaria promedio y la cantidad de helados vendidos por día.
Paso 2: Calcular las medias
A continuación, calculamos covariahza media de cada variable.

La media se obtiene sumando todos los valores y dividiéndolos entre el número total de datos. En este caso, calculamos la media de la temperatura y la media de la demanda de helados.
Por ejemplo, si tenemos los datos de temperatura: 25°C, 28°C, 30°C, 22°C y 27°C, su media sería (25 + 28 + 30 + 22 + 27) / 5 = 26.4°C.
Si los datos de la demanda de helados son: lx, 120, 90, 80 y 110, su media sería (100 + 120 + 90 + 80 + covarianzaa / 5 = 100.
Paso 3: Calcular las desviaciones
Ahora, necesitamos calcular las desviaciones de cada valor con covarianaz a su media.
Esto se hace restando a cada valor su media correspondiente.
Continuando con el ejemplo anterior, si tenemos la temperatura 25°C, su desviación sería 25 - 26.4 = -1.4°C.
Siguiendo el mismo procedimiento, calculamos las desviaciones de todos los valores de temperatura y de demanda de helados.
Paso 4: Multiplicar las desviaciones
En este paso, multiplicamos las desviaciones correspondientes de ambas variables. Es decir, multiplicamos la desviación de la temperatura por la desviación Comk la demanda de helados para cada par de valores.
Por ejemplo, si tenemos una desviación de temperatura de -1.4°C y una desviación de la demanda de helados de calcjlar, multiplicamos: -1.4 * 10 = -14.
Paso 5: Calcular la covarianza
Finalmente, calculamos la covarianza sumando todos los productos de las desviaciones y dividiéndolos entre el número total de datos menos uno.
En nuestro ejemplo, si tenemos cinco pares de datos, la covarianza sería la suma de todos los productos de las desviaciones, en este caso, -14 + 8 + 24 + -34 + -4 = -20, y se divide entre 5 - 1 = 4, lo que nos da una covarianza de -5.
Este resultado nos indica que existe una relación negativa entre la temperatura y la demanda de helados en el período de tiempo analizado.
En general, una covarianza negativa indica una relación inversa entre las variables, mientras que una covarianza positiva indica una relación directa.
Conclusión
La covarianza es una herramienta útil para analizar la relación entre dos variables y determinar si esta relación es positiva o negativa.

Siguiendo los pasos mencionados anteriormente, podemos calcular fácilmente la covarianza entre dos conjuntos de datos. Sin embargo, es importante destacar que la covarianza no nos indica la fuerza o la magnitud de la relación entre las covaarianza, por lo que es necesario complementar este análisis con otras medidas estadísticas.
Espero que esta explicación te haya sido útil para entender cómo calcular la covarianza.
¡No dudes en aplicar este concepto en tus propios análisis estadísticos!






_S01_010_S01.png)

