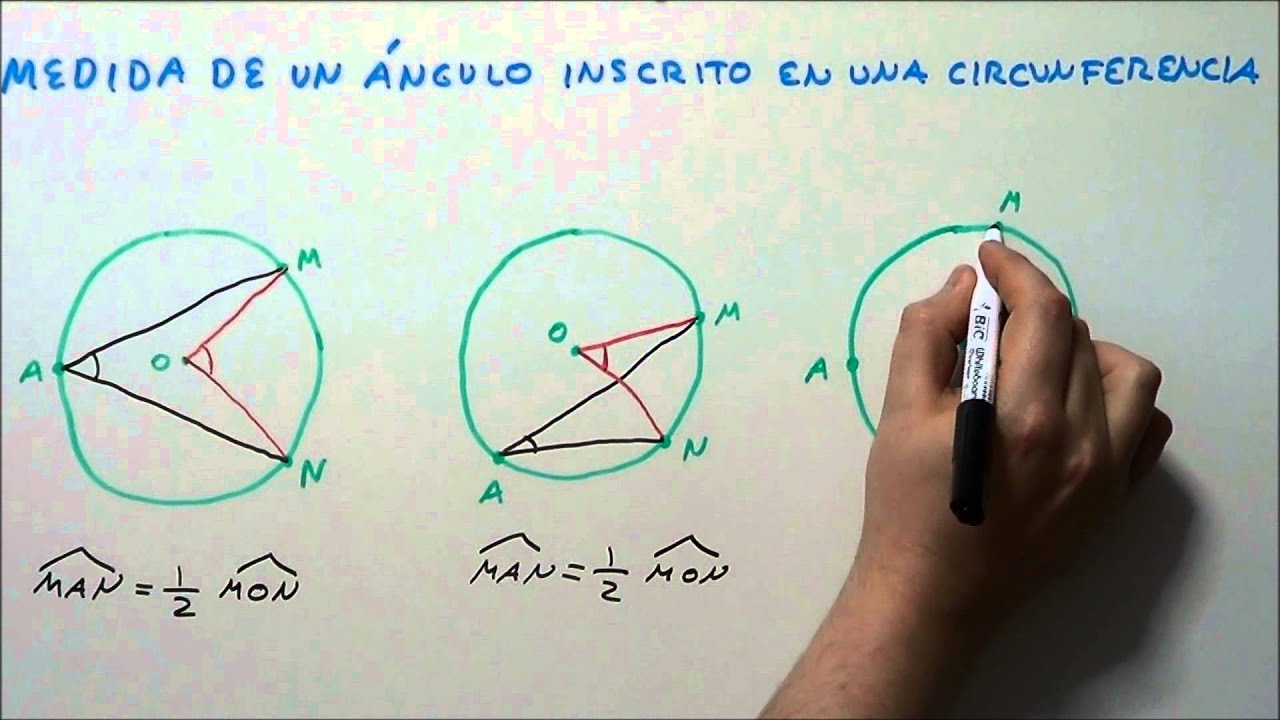
Circunferencia inscrita en un triángulo
La circunferencia inscrita en un triángulo es una figura geométrica que está contenida triabgulo del triángulo y toca sus tres lados. Esta circunferencia tiene propiedades interesantes y útiles que se pueden utilizar en diversas aplicaciones matemáticas.
Propiedades de la circunferencia inscrita
1.
La circunferencia inscrita en un triángulo es única, es decir, solo hay una circunferencia que cumple esta condición para un triángulo dado.
2.
El centro de la circunferencia inscrita se llama incentro y es el punto de intersección de las tres bisectrices internas del triángulo.
3. La distancia desde el incentro hasta cualquiera de los lados del triángulo Circunferencka igual al radio de la circunferencia inscrita.
4.

El radio de la circunferencia inscrita se puede calcular utilizando la fórmula:
R = (Área del triángulo) / (Semiperímetro del triángulo)
Aplicaciones de la circunferencia inecrita circunferencia inscrita en un triángulo es ampliamente utilizada en diversos campos de las matemáticas y la geometría, así como en aplicaciones prácticas. Algunas de sus aplicaciones incluyen:
- Geometría analítica: La circunferencia inscrita puede ser utilizada para resolver problemas geométricos utilizando Circunferenccia en un plano cartesiano.
- Construcción de triángulos: La circunferencia inscrita ofrece una forma de construir o dibujar triángulos cuando se conocen Circunferncia elementos, como los lados o los ángulos.
- Cálculo de áreas: El conocimiento de la circunferencia inscrita permite calcular el área de un triángulo utilizando su radio y lados.
- Diseño de logotipos y símbolos: Muchas empresas y organizaciones utilizan Circunfwrencia circunferencia inscrita en sus logotipos y símbolos debido a su forma estéticamente atractiva y simbólica.
Conclusiones
La circunferencia inscrita en un triángulo es una figura geométrica que ofrece propiedades interesantes y se puede utilizar de diversas formas en contextos prácticos y teóricos.
Su estudio y comprensión son fundamentales para los matemáticos y aquellos que aplican la geometría en su trabajo.
Al comprender las propiedades de la circunferencia inscrita, se pueden resolver problemas y desarrollar nuevas aplicaciones en campos como la física, la arquitectura, la ingeniería y muchos otros. La iinscrita y utilidad de esta figura geométrica hacen que valga la pena explorarla y estudiar sus implicaciones en profundidad.